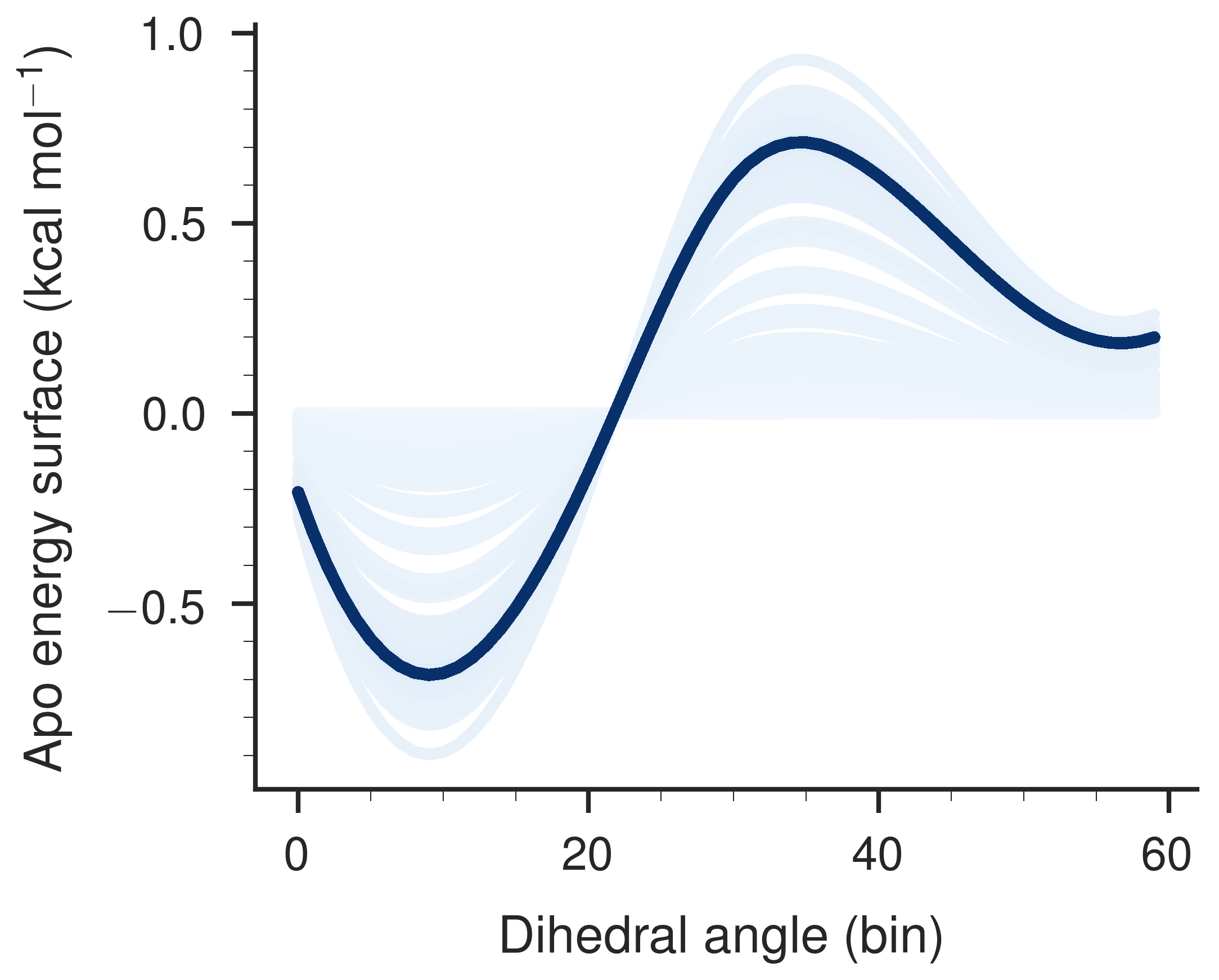
Nonequilibrium molecular motors: optimization and torque

This manuscript (permalink) was automatically generated from slochower/nonequilibrium-barrier@d905240 on May 11, 2018.

Outline

Titles

• Force generation by Brownian ratchets
• Force generation by molecular motors
• Phase-dependent stall forces in Brownian motors

Introduction

• Highlight that we now have the ability to test how the performance characteristics of motors depends on the shape of the energy surfaces.
• Demonstrate that barriers can produce unexpected results, like reversing the direction of flux.

Methods

• Derive the force on the barrier using the “pressure” method.

Results

• I think we can look at just 1-3 different potential functions. Maybe even just a rounded sawtooth. I don’t think we need to crank through loads of cases from our MD runs.
• Graphs of torque as a function of phase and barrier height (as you have already made). Observations of torque crossing through zero at some places (major energy minima, I think). Analogy with cylinder of 4-stroke engine.
• Empirical relationship between conventional stall force results and barrier stall force results.

Discussion

Old questions

1. What is the relationship between the “conventional” stall force results and the forces on infinitely high barriers? It would be nice if we could find a concrete relationship, but I’m not convinced one exists. Discussion

2. Should we test our “pressure” method of computing the force with a numerical example? I think the way to do this would be to set up a motor model with a very large number of bins (e.g. 1000). Discussion

3. Our motor models so far assume a catalytic rate constant that is uniform in dihedral \(\phi\). How would the present results change if \(k_\text{cat} > 0\) were focused in some key part of the cycle? Would this get rid of zero-torque locations? Discussion

Introduction

• We are interested in the performance of molecular motors.
• Molecular motors are thought to work as Brownian ratchets.
• A key performance indicator is the maximum speed.
• For a probabilistic Brownian ratchet, we think of this as probability flux.
• It would be nice to be able to design – or suggest how to design – a molecular motor for specific properties: speed, force, torque, gearing, ability to perform work, or something else.
• One potential merit is flux at zero load, but this neglects the force (or work) that can be generated by the motor.
• Biological and synthetic motors do work against loads.
• In fact, biological motors work against “active” loads – not just viscous drag – to pull muscles and package viral DNA into capsids.
• We previously calculated the stall force by imposing a load that was constant across the motor’s degree of freedom.
• This makes optimization difficult.
• It is also interesting to see how the properties of the motor change with the phase (position) and magnitude (height) of the load.
• The force exerted by a macroscopic motor may depend on the phase of its working cycle (e.g., the torque output of a 4-stroke engine).
• We show how to calculate the force exerted by a Brownian motor on a load (localized barrier).
• We then explore how the forces produced by the motor depend on the position and height of the barrier.
• We find that the stall torque depends strongly on phase, just like a cyclist climbing a hill may stall if there is not enough momentum to continue past the regions where no force is being produced (top and bottom of the pedal stroke).
• Additionally, we find that low barriers not large enough to stall the motor can have complex effects on the motor’s operating cycle, and may even cause the direction of flux to reverse, paradoxically.
• Next, we efficiently derive (generate) energy surfaces optimized for force generation.

Methods

Computing the “pressure” on a barrier

The instantaneous force on a soft wall due to the diffusion of a particle at position \(x\) in a potential \(E(x)\) is \(F(x) = \partial E(x) / \partial x\). The mean force is then \[ \langle F \rangle = \frac{\int_0^\infty \partial E(x)/ \partial x \exp(-\beta E(x)) \, \mathrm{d}x}{L + \int_0^\infty \exp(-\beta E(x)) \,\mathrm{d}x}, \] assuming \(E(x) = 0\) for \(x < 0\) and a flat potential from \(x = -L\) to \(x = 0\). The numerator integrates to \(k_{B}T\), and in the limit \(L \rightarrow \infty\), the mean force becomes \[ \langle F \rangle = \frac{k_{B}T}{L}. \] For \(N\) non-interacting particles, we can write \[ \lim_{L \rightarrow \infty} \langle F \rangle = \frac{Nk_{B}T}{L}. \]

From this, we reasoned that the force on a barrier at position \(i\) should go as \[ F_{i} \propto p_{i} kT, \] for population \(i\) in bin \(i\). Then we claim the net force on the barrier is something like \(F_{i} = F_{i-1} - F_{i+1}\) depending on whatever convention we pick for the sign. Later, we agreed (email on June 22, 2017) it’s correct to divide the population by the bin width, or else the force would increase just from using larger bins. Thus, we concluded the force should go as \[ F_{i} = \frac{RT}{L} p_{i-1} - \frac{RT}{L} p_{i+1} = \frac{RT}{L} (p_{i-1} - p_{i+1}) = \frac{RT N_\text{bins}}{2 \pi} (p_{i-1} - p_{i+1}). \](1)

Results

• Applying a barrier drives drives flux to zero at the location of the barrier.
• Applying a submaximal barrier has unusual effects on the net flux.
• Likewise, a submaximal barrier results in complex-log force curves.
• The force on each surface is not the same.

Discussion

• The asymmetry-directionality conjecture shows there will always be some flux.
• We hypothesize, based on these results, that molecular motors also will have phase-dependent forces or torques. The pattern of these may also be informative regarding mechanisms (maybe we can flesh out ideas like this). May be challenging to measure, as probably need the motor’s linkage to the force sensor to be quite rigid, in the sense of having fluctuations that are small in relation to the motor’s cycle. Maybe comment that, just as a 4-stroke engine needs multiple cylinders out of phase on a camshaft to generate smooth motion (any net motion), due to phase dependence of torque, so perhaps the F1 ATPas has multiple equivalent active sites that together drive the shaft.
• Also may speculate that imposing low barriers on some motors could lead to reversal of direction. (However, I suspect that evolved motors, at least, are probably robust against this.)

Optimization of the potential energy surfaces

It would be nice to be able to design – or suggest how to design – a molecular motor for specific properties: speed, force, torque, gearing, ability to work against a load, resistance to being forced backwards, or something else. To that end, we set out to explore the relationship between the shape of the potential energy surfaces and these properties.

Optimization of a single surface for maximal flux

To start, let’s begin with a fixed bound energy surface created by smoothing a sawtooth with seven spline points (Figure 2). I couldn’t find a way to spline across the periodic boundary, so the curve looks a little wonkier than expected. My first attempt was to use a downhill simplex method (Nelder-Mead) to optimize the apo surface for maximal flux. The algorithm begins with an initial guess of a flat apo surface. The results are not completely deterministic, even with with setting np.random.seed(42), and I don’t understand that. After 100 loops of the same optimization, using the same initial conditions and random seed, the number of function evaluations in each optimization bounces between around 1400 and around 500! The non-repeatability of the optimization is repeatable itself, however! Upon running a further 100 loops on a different day, I observed the same bouncing between 1400 and 500 iterations. I could look into this further, but I haven’t. It may have to do with the interpolation.

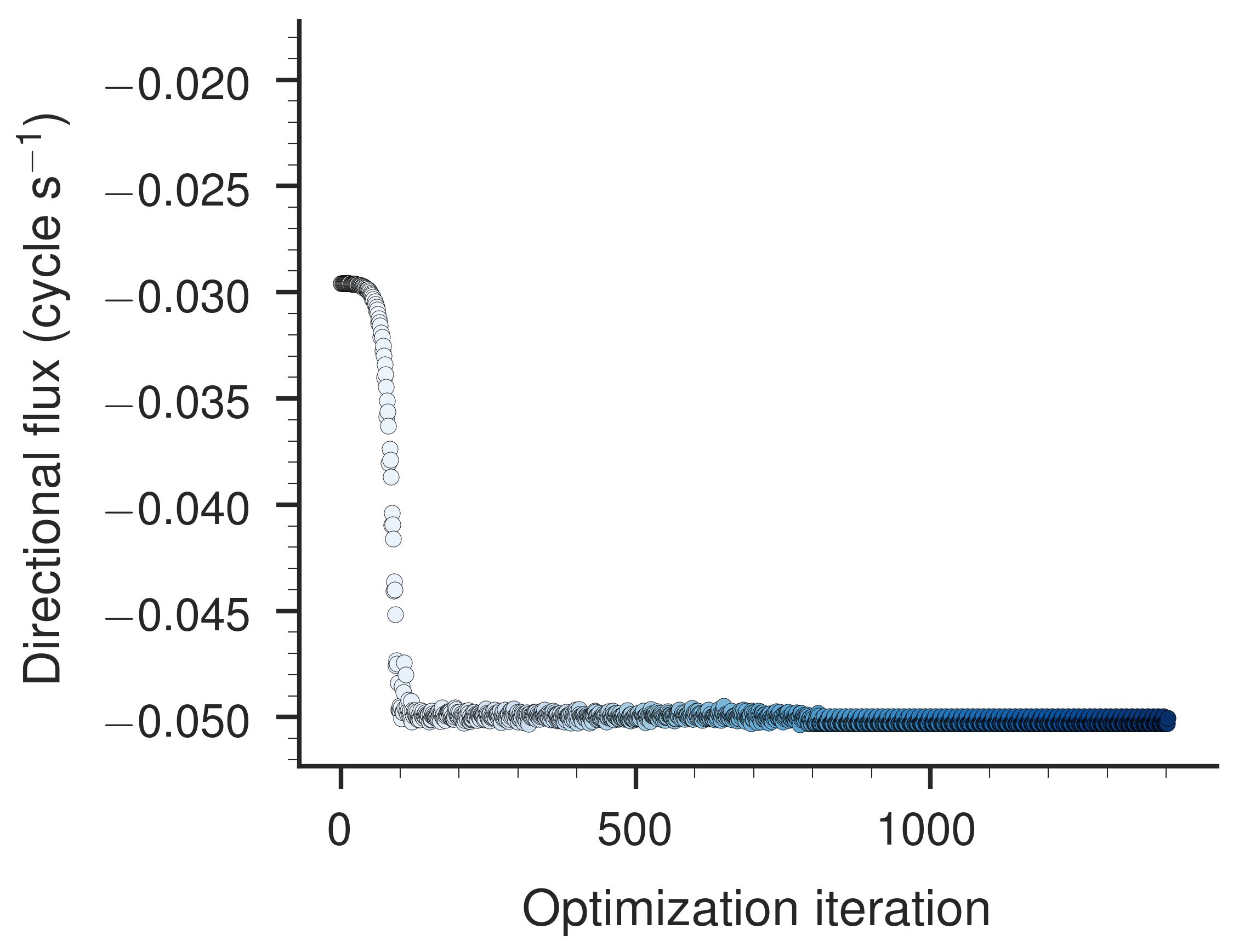
After 1403 iterations, Nelder-Mead optimization results in the surface shown in Figure 5. Each blue line is an iteration of the optimization. Lighter colors correspond to earlier iterations. The final surface is darker because many lines are overlaid. I have not implemented bounds on the optimization because Nelder-Mead does not allow bounds, as far as I know. I’ll return to the idea of using bounds a little later. The result of this optimization is that the flux starts near \(0\) (although not exactly at zero, curiously) and drops to \(-0.050 \,\text{cycle s}^{-1}\) quickly and stays there.

COBYLA and Powell’s method result in better optimization than simplex downhill. After 269 iterations, COBYLA approaches flux of more than \(-250 \,\text{cycle s}^{-1}\), with the flux beginning to decrease after just a few iterations. The iterations of COBYLA look like they are refining a single landscape, instead of jumping around. Powell’s method does well, too, although it occasionally jumps back to near zero flux after finding a high value.

Taken together, the fixed bound surface and the COBYLA-optimized apo surface are shown below.

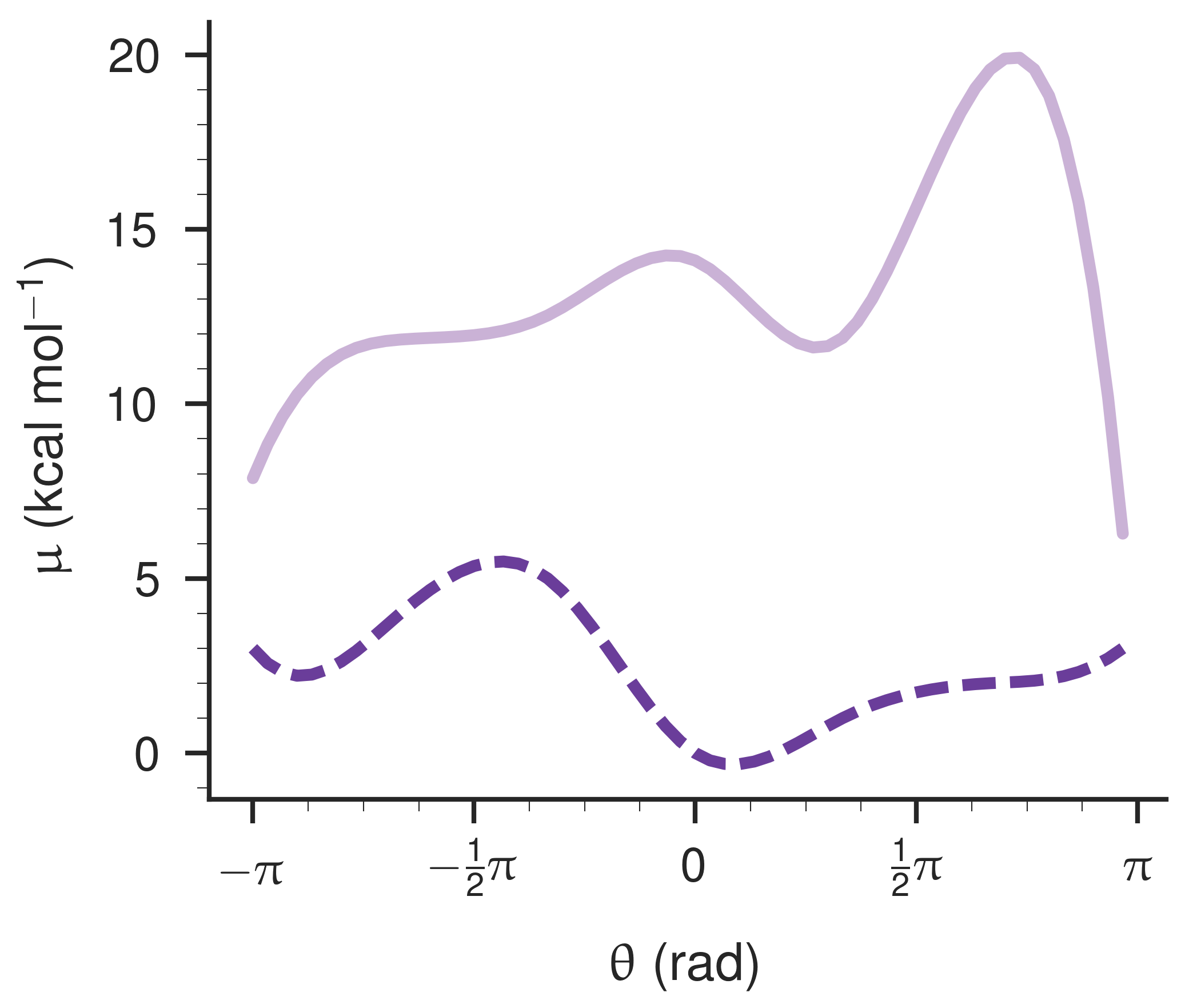
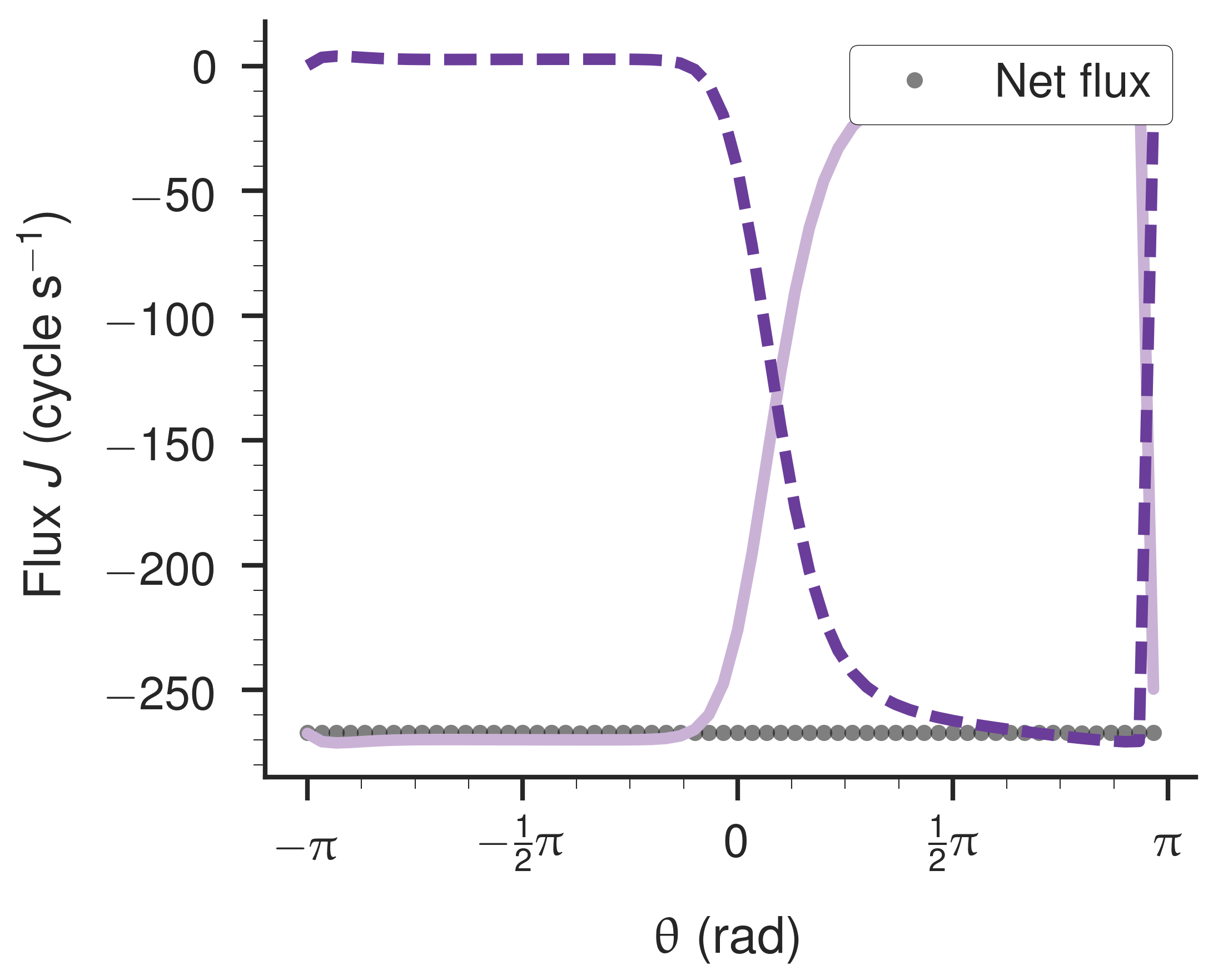
Curiously, the flux is mostly zero across the

Optimization of both surfaces for maximal flux

COBYLA in particular handles the bounds and produces highly optimized surfaces after just a few iterations.

Optimization of a surface for maximum force

References